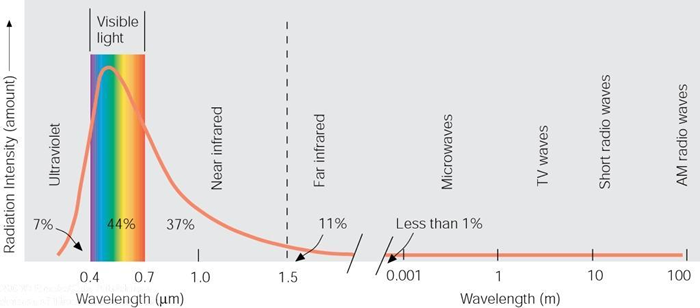
The only true source of energy on the earth is the sun. The fossil fuel we burn is simply stored energy from the sun. The energy is first transformed into a carbon form through the process of photosynthesis. The transfer of energy from the sun is in the form of electromagnetic radiation. Radiation transfer has both wave-like and particle-like behavior. Evidence of its wave-like behavior is seen in the refraction of light through a prism where the amount of bending of light depends on the wavelength of the light. The wavelength distribution of our sun's radiation is shown in the figure below. Note that the majority of the radiation is in the "visible" range - the radiation that our eyes can "see." The shorter the wavelength, the more energetic the wave. Consequently, radiation in the ultraviolet region is damaging to our skin when it is absorbed. Fortunately, the earth's stratosphere is home to sufficient quantities of ozone that absorb must of the ultraviolet radiation before it reaches the surface of the earth.

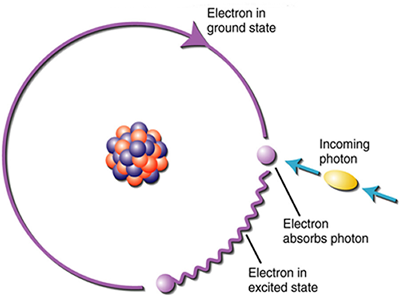
Evidence of the particle behavior of radiation includes the fact that radiation is able to travel through a vacuum. Wave-like behavior requires a medium such as water or air. Further evidence of particle-like behavior involves the absorption and emission of radiation by atoms. The wave particles are called "photons" which excite the electron motion of the atom when it is absorbed. The bundle of radiation energy is emitted when the electron "falls" back to its original energy state. This process is shown in the figures below.
|

|
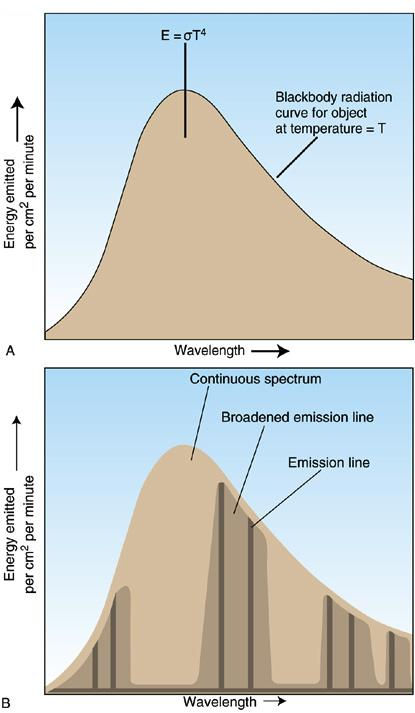
Solid objects (you, me, a desk, the earth, the sun) that absorb radiation at all energy levels, or wavelengths, and re-emit all of the radiation are called "blackbody radiators." The associated blackbody radiation spectrum depends on the surface temperature of the object. Spectrums for different objects are shown in the figure below.
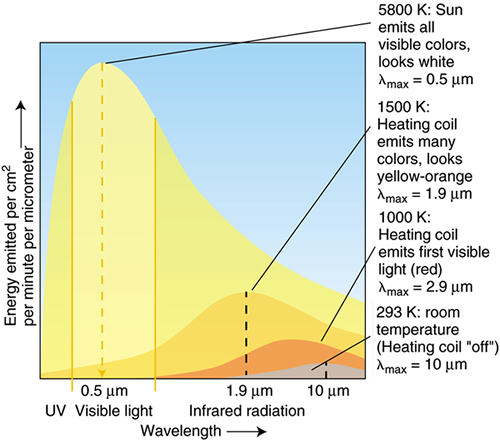
Note that the wavelength at which the maximum amount of energy is emitted is different for each body. In fact, this maximum wavelength is given by Wien's Law which is
$\lambda_{max} = 2890/T$
The area under the curve represents the total energy per area (square meter or square centimeter) the blackbody is emitting (see figure A below). The Stefan-Boltzman formula gives this value as
$ E = \sigma T^4$,
where $\sigma$ is the Stefan-Boltzman constant and $T$ is the temperature of the body's surface.
|
|
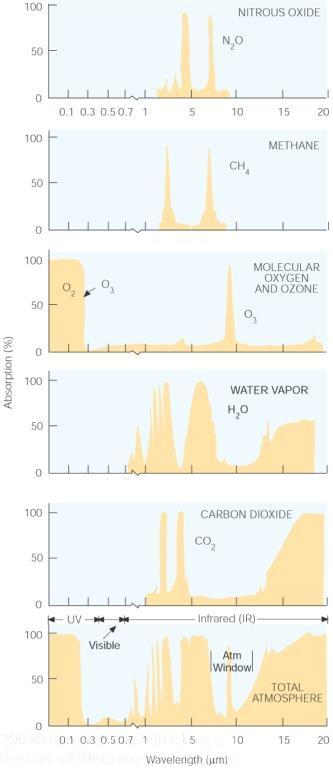
Gasses in the earth's atmosphere absorb and emit radiation at discrete energies or wavelengths. An example of a radiation curve is shown in figure B above. The prominent greenhouse gasses selectively absorb and emit radiation as indicated in the figure to the right above. Note how the ozone absorbs almost all of the solar radiation in the ultraviolet region as mentioned above. The earth's atmosphere is virtually transparent to solar radiation in the visible range. This means almost all of the sun's radiation in this range reaches the surface of the earth. Here it is absorbed and the emitted because of the blackbody nature of the earth. However, because the earth is much cooler than the sun, the emission spectrum is shifted significantly to the longer wavelength regime. Certain wavelengths (energy levels) are absorbed by the different greenhouse gasses. Note that there is an atmospheric "window" is this region as well. The combined atmospheric effect is indicated in the bottom-most pane on the right. Here we can see that the earth's atmosphere is almost opaque to the longer wave infrared radiation that is emitted from the earth's surface.
What does this "greenhouse gas blanket" mean in terms of the earth's temperature? First, let us consider the case without any such effect. The figure below shows the result in this case. In this scenario the earth's surface temperature would be about -18 degrees Celsius (zero degrees Fahrenheit).

When the returning radiation from the greenhouse gasses is included, as indicated in the figure below, the earth's average temperature is something like $15^o$ C when the system reaches equilibrium.
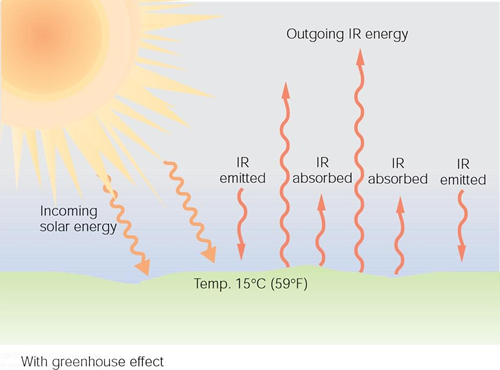
This result is well-described by David Archer through the use of a single slab model. Click here to view this explanation. A slimmed down version is available here.
Next we will consider a more comprehensive view of energy considerations involving the incoming solar radiation, the earth's atmosphere, and the earth's surface. We begin by supposing 100 units of energy are passing through an area of, say, one square meter. In actuality, the earth receives something like 340 W/$m^2$ on average, but we will use "100" because it is a better number for sake of accounting. Further, we will assume that the system is in equilibrium which means the average temperature of the atmosphere and the earth is constant in time.
The first consideration is the "albedo", or reflectivity, of the atmosphere and earth surface. This is the amount of incoming energy that is simply reflected back to outer space. Because it is not absorbed, no warming occurs, and no additional consideration is necessary. Reflection primarily occurs at the top of the atmosphere, off white (high, cold ice-crystal) clouds, and the surface of the earth. The respective amounts for each of these are shown in the figure below. All told, about 30% of the incident solar radiation is reflected back to outer space.
The remaining 70 units are absorbed by either the atmosphere (19 units) or the earth (51 units). It may be helpful to think of these components as separate "stores" of energy. The energy within these stores translates directly to the temperature of the component. If the temperature of, say, the earth is constant over a long period of time, then the earth must emit as much energy as it absorbs. The same must be true about the atmosphere.
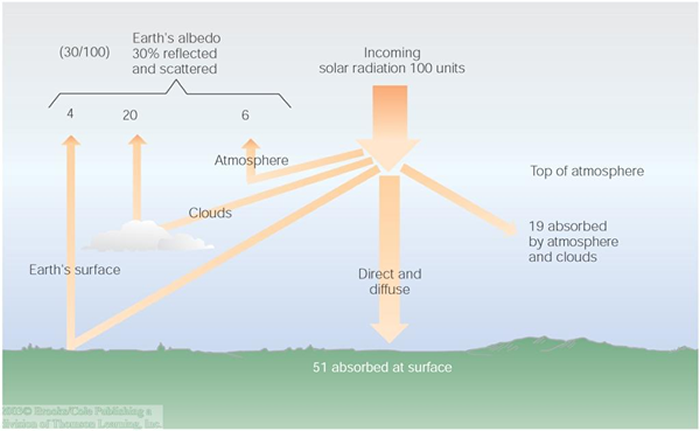
We know the earth is a rather efficient blackbody and emits much, if not all, of the energy it receives. And, we know the green house gasses in the atmosphere absorb much of this infrared energy and return some of it to the earth's surface. The figure below shows this returned radiation measures something like 96 units. In sum then, the earth receives 147 units of energy.
Under the assumption of constant temperature, the earth must "give up" 147 units of energy to equal the inflow. We already know one such mechanism for energy transfer is radiation. Through the use of satellite measurements and assumptions of equilibrium, the net radiation loss from the earth's surface is 117 units. This includes radiation that is absorbed by the atmosphere as well as that which is lost to outer space.
Two additional energy transfer mechanisms account for the other 30 units the earth most give up. Evaporation (changing water from liquid to gas) of water accounts for 23 units. This process is often deemed "latent" heat transfer because one would not truly "sense" a change in energy. That is to say, moist air at 70 degrees fahrenheit has more energy associated with it than dry air at the same temperature. But the thermometer, the sensor, indicated the same temperature.
Convection and conduction are, actually, two entirely different process. They are lumped in this case because they represent "sensible" energy transfer. The conduction process causes the handle of a cast iron skilled to get too hot to grab with your bare hand. Energy is transfered on the molecular scale as the warmer, more energetic, molecules nearer the heat source smash into adjecent cooler molecules and transfer their kinetic energy. This "motion" energy is what we measure when the temperature is determined. Conduction involves the motion of masses of fluid from warmer to cooler regions. The conduction process warms most homes.
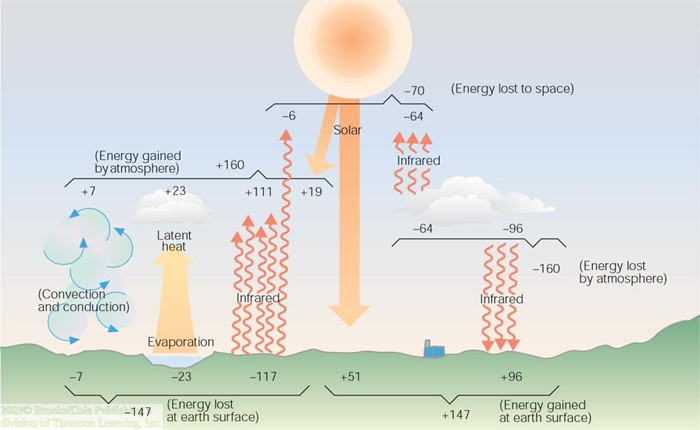
Note that the energy budget in the figure above indicates the atmosphere gains 160 units of energy through radiation, latent heat transfer, and convection/conduction processes. The same amount of energy is given up through radiation.
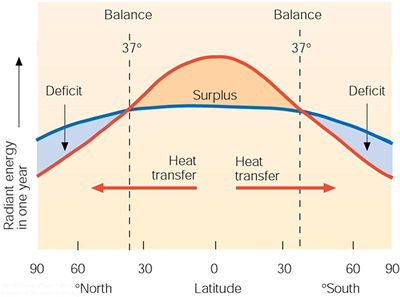
The energy budget described above is a globally averged scenario. In reality, very few locations on the surface of the earth would exhibit a balanced energy system as outlined above. Not surprisingly, regions closer to the equator would show an energy surplus over time, and those closer to the poles would show an energy deficit over time. The figure below shows the distribution of "long-term" energy surpluses and deficits as a function of latitude for the earth. The question now arises: Why don't the surplus (equatorial) regions continue to warm and the deficit (polar) regions continue to cool? We'll try to answer this question next as a way to understand the general circulation of the atmosphere as one aspect of the earth's climate.